FP2級技能士のきのこです。
FPの勉強を開始して、早速つまづくのが「6つの係数」ではないでしょうか。
「似たような名前で、毎回混乱する！」「覚えられない！」と、苦手意識がある人も多いと思います。
本記事では、6つの係数について徹底的に解説し、覚え方・実際の試験での解き方・どうしても覚えられない場合の裏技をお伝えします。
この記事さえ読めば、あなたの苦手意識は克服されること間違いなしです。
では、さっそく見ていきましょう！
6つの係数とは
① 終価係数
複利運用をした場合の一定期間後の金額を求める
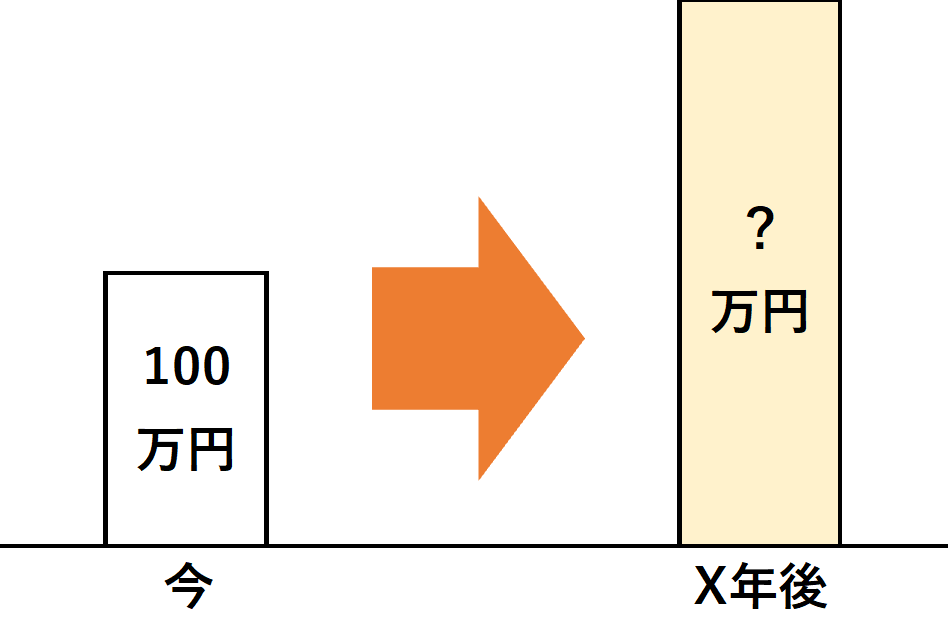
② 現価係数
一定額に達するために必要な元本を求める
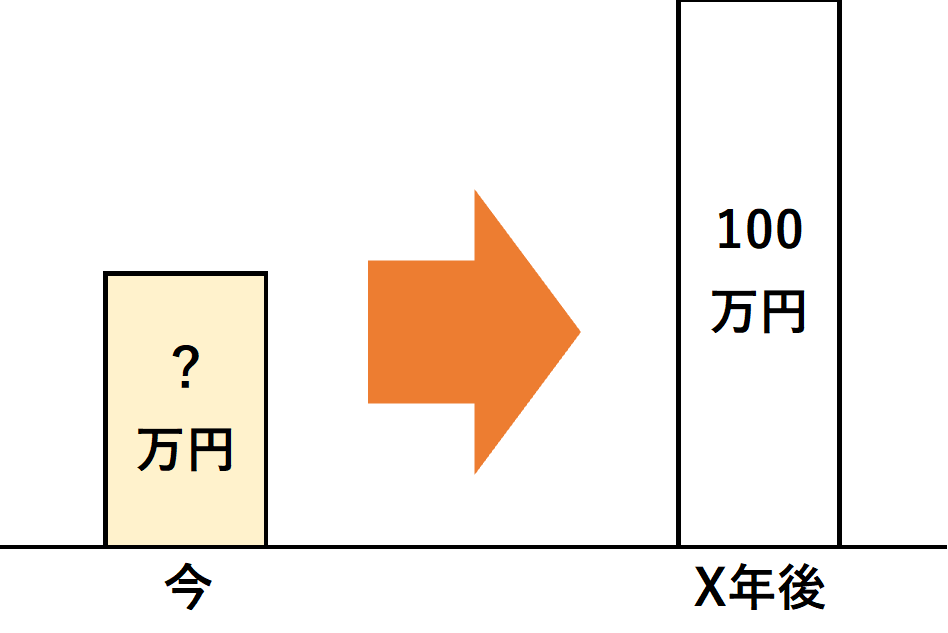
③ 年金終価係数
毎年一定額を積み立てた場合の一定期間後の金額を求める
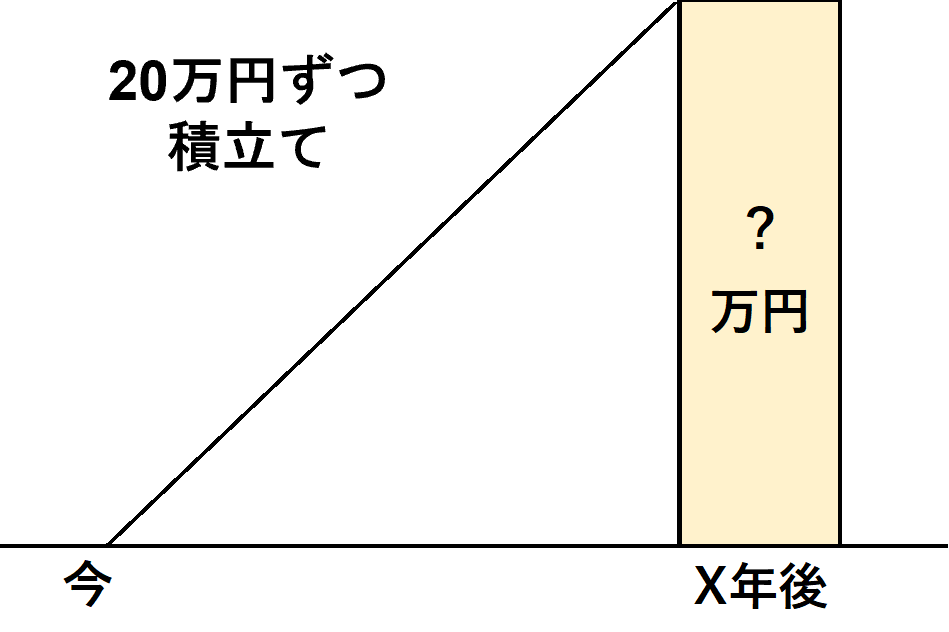
④ 減債基金係数
一定額を用意するための毎年の積立額を求める
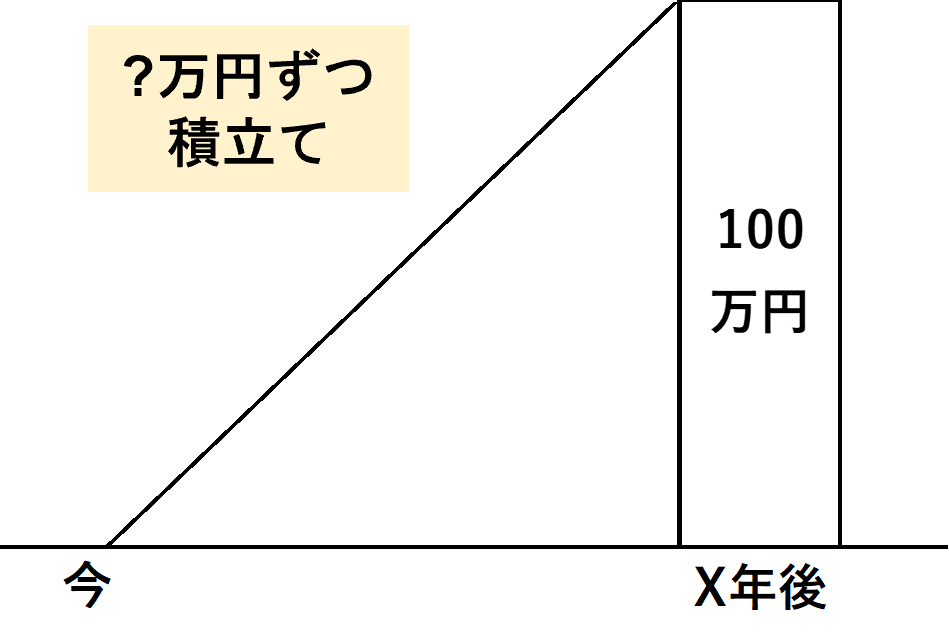
⑤ 資本回収係数
一定額を一定期間で取り崩した場合の毎年の受取額を求める
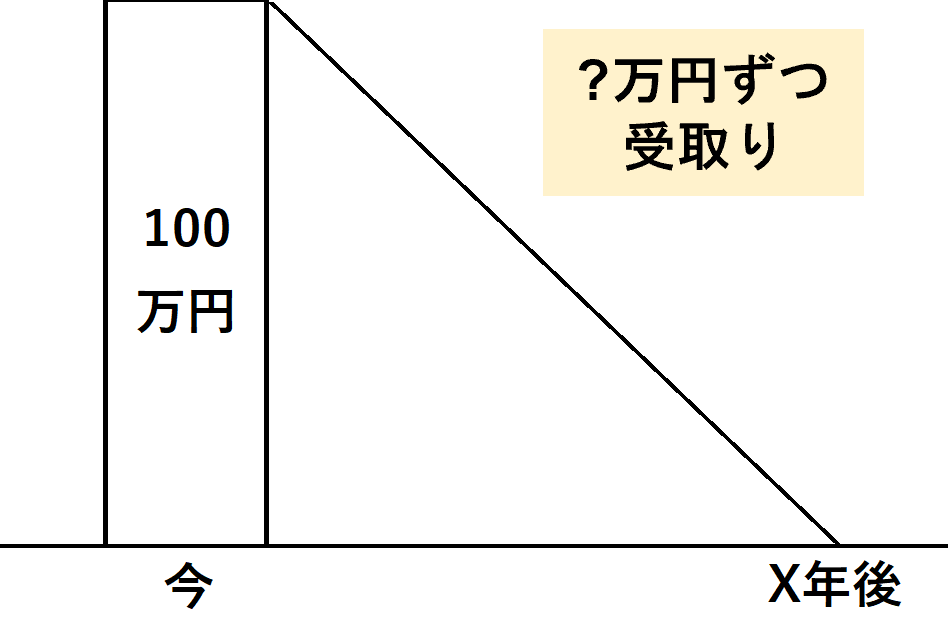
⑥ 年金現価係数
将来、一定期間にわたり一定額を受け取るための元本を求める
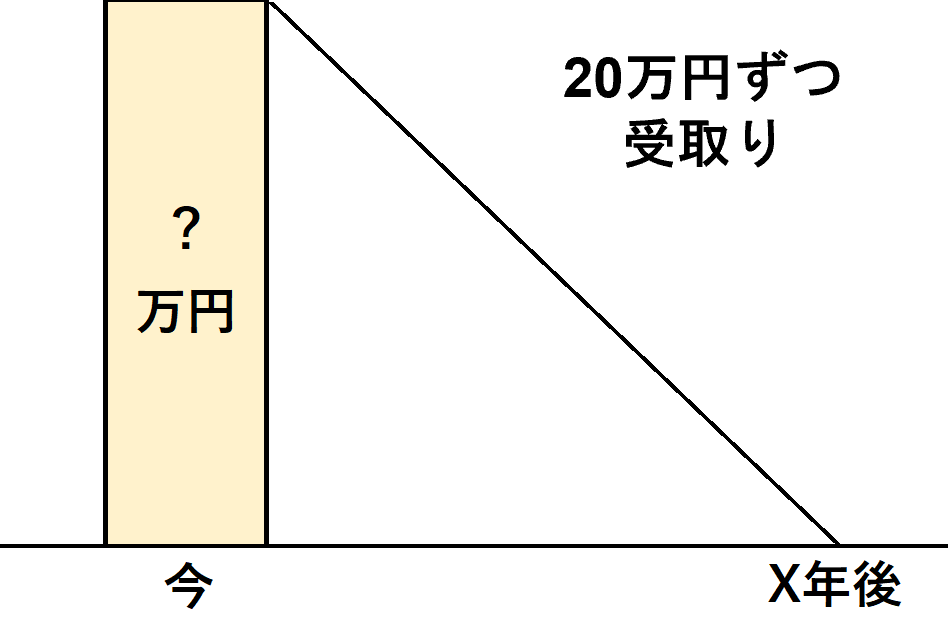
さて、ここまではテキストにも載っている内容だと思います。
文言で覚えるのではなく、図のイメージをしっかり持つよう意識してください。
6つの係数 攻略法 3つのStep
では、具体的にどのように攻略をしていくのか、3つのStepに分けて解説します。
Step① 3つのペアを作る
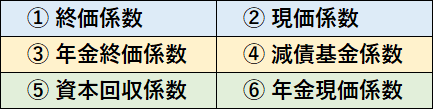
この並びを頭に叩き込んでください。
表で、横に並んでいるもの同士がペアとなります。
では、少し恥ずかしいですが、私の覚え方を紹介しますね。
注意点は、①終価係数と②現価係数がペアなのに、③年金終価係数と⑥年金現価係数がペアではない、というところです。
6つの係数をややこしくしている原因はここにあるかもしれません。
Step② ペアとキーワードを結び付ける
それぞれのペアごとに、関連するキーワードがあります。
というように、キーワードと係数を結び付けられるようにしましょう。
Step③ 将来を知りたいか/現在を知りたいかを判断する
では、①②の使い分け、③④の使い分け、⑤⑥の使い分けはどのようにするかを解説します。
先ほどのペアの表をもう一度見てください。
実は、この表の左右で、将来を知りたいか/現在を知りたいかが分けられています。
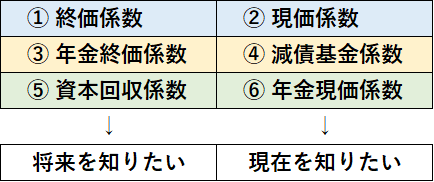
如何でしょうか。少し頭が整理されたかと思います。
覚え方は、「ゲンカ・ゲンサイ・ネンキンゲンカ＝ゲンザイを知りたい」です。全て「ゲン」が付きますね。
対して、「シュウカ・ネンキンシュウカ・シホンカイシュウ」には濁点すらつきません。
6つの係数 問題の解き方
まず、FP試験において6つの係数が問題になる場合、以下の2パターンがあります。
パターン①
「XXXXを求める場合、使用する係数として正しいものは次のうちどれか。」という問題
(例)
元金を一定の利率で複利運用しながら、毎年一定金額を一定の期間にわたり取り崩していくときの毎年の取崩し金額を計算する場合、元金に乗じる係数は、( )である。
1. 現価係数
2. 減債基金係数
3. 資本回収係数
(2022年1月 FP3級試験 学科 問31)
パターン②
「XXXXの場合、XXXXはいくらになるか。次のうち適切な係数を使用して算出せよ。」という問題
(例)
900万円を準備するために、15年間、毎年均等に積み立て、利率(年率)1％で複利運用する場合、必要となる毎年の積立金額は、下記の<資料>の係数を使用して算出すると( )である。
1. 516,780円
2. 558,900円
3. 600,000円
(2020年9月 FP3級試験 学科 問31)
- パターン①の場合…先ほどの3つのStepを思い出しながら答えを導く方法しかありません。
- パターン②の場合…実は係数を覚えなくても、解く方法があります。
しかも出題は、②の形式であることがほとんどです。
ここでは、パターン②における問題の解き方・裏技について、例題を使って解説します。
(例題1)
900万円を準備するために、15年間、毎年均等に積み立て、利率(年率)1％で複利運用する場合、必要となる毎年の積立金額は、下記の<資料>の係数を使用して算出すると( )である。
1. 516,780円
2. 558,900円
3. 600,000円
(2020年9月 FP3級試験 学科 問31)
真面目な解き方
- 積み立てときたら、③年金終価係数 ④減債基金係数 のどちらか
- 毎年の積立金額＝現在のことを知りたいので、④減債基金係数
⇒ 900万円 × 0.0621 = 558,900円
裏技！
- 15年かけて900万円を準備するためには、普通は1年あたり 900万÷15年＝60万円 の貯蓄が必要
- しかし、複利運用(1%)した結果900万円になるということは、「年間60万円より少しだけ少なくてもOK」ということ
⇒ 558,900円
(例題2)
元金3,000万円を利率(年率)1％で複利運用しながら、15年間にわたって毎年均等に取り崩して受け取る場合、毎年の受取金額は( )である。なお、計算にあたっては下記<資料>の係数を使用して算出するものとする。
1. 1,863,000円
2. 2,163,000円
3. 2,322,000円
(2019年9月 FP3級試験 学科 問31)
真面目な解き方
- 取り崩しときたら、⑤資本回収係数 ⑥年金現価係数 のどちらか
- 毎年の受取金額＝将来のことを知りたいので、⑤資本回収係数
⇒ 3,000万円 × 0.0721 = 2,163,00円
裏技！
- 3,000万円を15年にわたって取り崩すということは、普通は1年あたり 3,000万÷15年＝200万円 受け取ることができる
- しかし、複利運用(1%)していくわけなので、「年間200万円より少しだけ多く受け取れる」ということ
⇒ 2,163,000円
(例題3)
借入金額300万円、利率(年率・複利)3％、返済期間5年、元利均等返済でローンを組む場合、毎年の返済額は、下記の<資料>の係数を使用して算出すると、( )である。
1. 565,200円
2. 655,200円
3. 695,580円
(2021年1月 FP3級試験 学科 問31)
真面目な解き方
- 300万円を返済する場合の毎年の返済額と、300万円を取り崩す場合の毎年の受取額は同じ考え方
- 取り崩しときたら、⑤資本回収係数 ⑥年金現価係数 のどちらか
- 毎年の受取金額＝将来のことを知りたいので、⑤資本回収係数
⇒ 300万円 × 0.02184 = 655,200円
裏技！
- 5年かけて300万円を返済するためには、普通は1年あたり 300万÷5年＝60万円 の返済が必要
- しかし、複利(3%)が乗っかってくるということは、「年間60万円より少しだけ多く返済しなくてはならない」ということ
⇒ 655,200円
695,580円の可能性もあるのでは？と思うかもしれませんが、提示された3つの係数のどれを掛けても、695,580円にはなりませんね！
まとめ
Step① 3つのペアを作る
Step② ペアとキーワードを結び付ける
Step③ 将来を知りたいか/現在を知りたいかを判断する
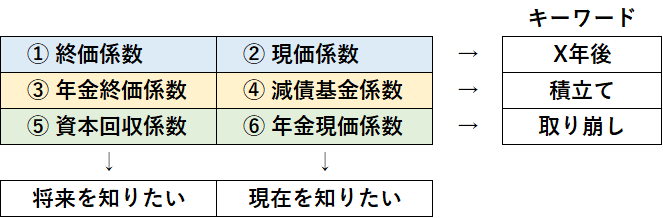
6つの係数は一見非常にややこしいですが、一度理解すれば難しいものではありません。
上の表が書けるようになれば、試験ではどんな問題でも解けるでしょう。
また、どうしても覚えられないという人は、ご紹介した裏技を使って解く練習をしましょう。これ、本当に便利ですよね。
実際の試験では1～2問の出題です。もしかしたら、「捨てようかな」と思われている方もいるかもしれませんが、もったいないですよ！
確実に取れる問題を積み上げていかなければ、合格には結び付きません。
混乱したら、二度三度とこの記事を見返して頂き、しっかりと身につけていきましょう。
また、FP3級の各科目について、以下の記事で解説しています。
併せてお読みください。
最後までお読み頂き、ありがとうございました！
